As many of you know…math is a passion of mine, and helping get kids excited about math is high on my list of goals every year. One thing I have learned in my more than 20 years in the classroom is that certain math “behaviors” must be in place before deep understanding takes place.
One thing that I have really started to notice, however, is MY role in making sure I am really checking for understanding. I have set it as a goal to really get better at the type of problems I ask of my students so that I can do a better job of seeing what they CAN do and what they cannot. The one thing I have recognized is that I need to a better job “fishing” for misconceptions–because the only way to clear up misconceptions is to find what they are! Let me show you a few examples of what I mean…and you can see how a few simple tweaks in how you ask questions can open up a WORLD of new information to you!
First of all…check out this simple but easy way to push students’ thinking–and see if YOU have missed anything in their understanding!
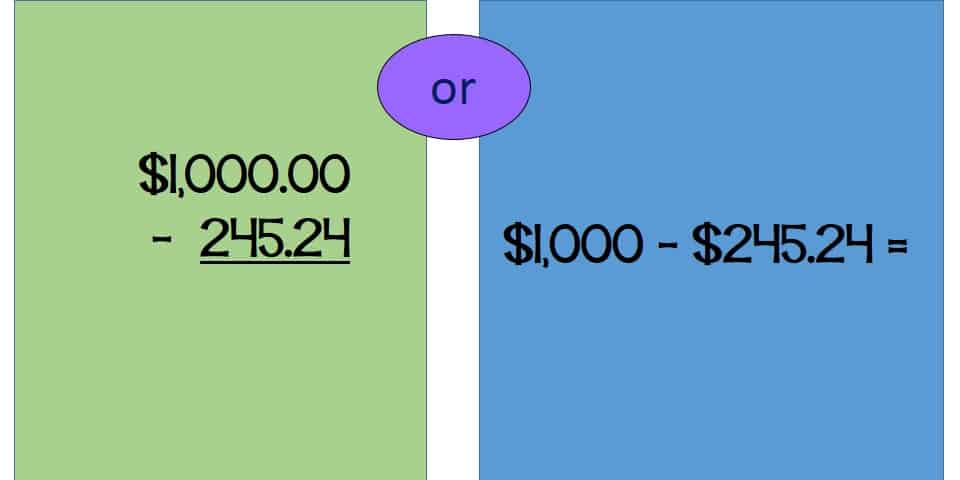
This might not seem like anything too shocking…but it really does change the problem dramatically. First of all, the first problem is all set up with the place value columns all line up. Simply by changing the presentation to “horizontal” rather than “vertical”, you can check to see if students have that understanding of “place”. Watch where they line up numbers. An easier lead in problem might be 683 – 59…no decimals there to trip them up! This one, however, was given to my students with a distinct purpose–to check to see if they can line up the thousands, hundreds, and so on…AND to see if they recognize the $1,000 as being $1,000.00. Guess what? Only 4 of my students got this problem right! I had errors in both places I suspected I might.
Looks like it’s time to reteach!
Here’s another one.
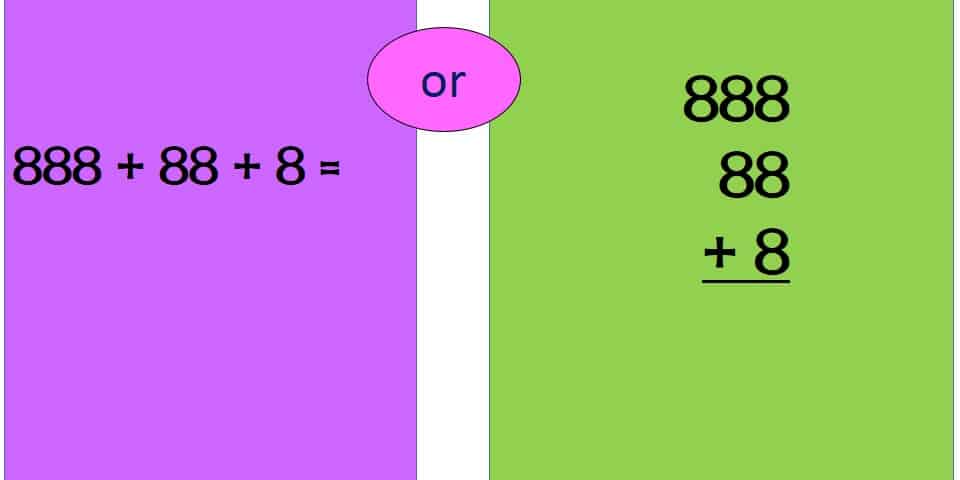
Same idea! Which is easier? The one on the right! It is set up for students to simply add the columns that have been set up nicely for them. The horizontal problem on the left forces them to consider place value when setting up the problem. You know what else this problem lets you check for? Do they know what to do when a “place” adds up to more than 19? Watch to see if students know what to do when they have to “carry” more than a “1”. Somehow misconceptions about this process show up more when we ask them to use numbers like this. “Carrying the 1” becomes automatic–we want to make sure students understand what is REALLY happening when they move numbers from place to place.

This is pretty obvious, right? Which type of problem are we most likely to see in a textbook? Which will give us the most information? I like to ask my students the question on the right to see their depth of understanding. If they draw a shape similar to the one on the left, I only know part of the story. Do they explain what they know about numerators and denominators? Does anyone show 1/4 on a number line? 1/4 of a set of objects? It gives me a much better picture of what they know–and a better sense of what needs to happen with my instruction. Let’s be honest–students have seen that picture on the left so many times that they may treat it like a “sight word”–they know it is 1/4 but have NO idea what that really means.
Finally, check out this one.
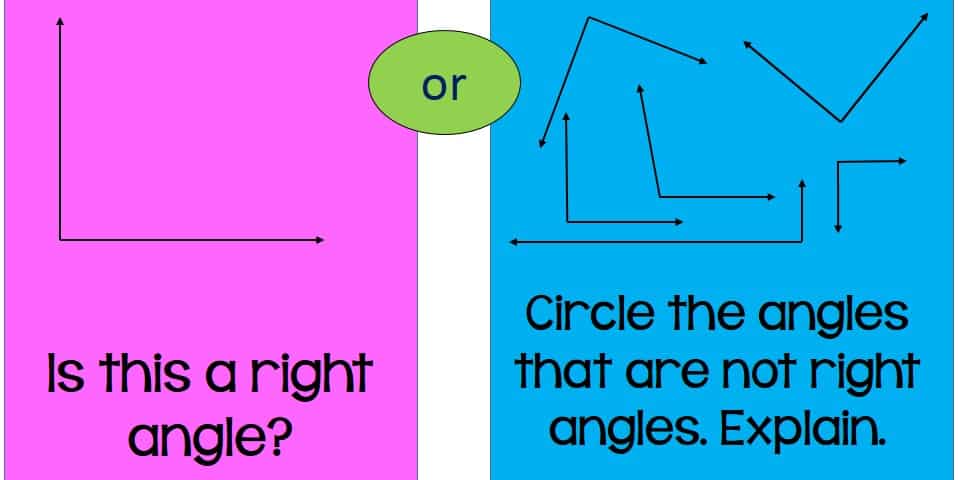
You might have seen problems that ask students to identify right angles–maybe even choose the right angles from a group of pictures. But guess what? Most of them have the rays the same length, have the angles all pointing “to the right” (did you KNOW that many students only think it’s a right angle if it faces that way?), and are “right side up”. In addition to understanding the concept of “right angle”, students also need to understand that angles can be rotated, that the rays can vary, and that the size of the rays is irrelevant (the arrow on the end shows that it goes on forever!). Many students see the right angle as being that picture on the pink–they don’t realize that angles are truly a measure of how “open” two rays are–no matter their position in space or the length of the “arms”. Giving them problems that force them to consider these misconceptions can help YOU make sure they don’t leave your classroom with faulty reasoning or incomplete math understanding.
Give these problems a try–and I’d love to hear about other other math misconceptions you uncover in YOUR classroom! Knowing what our students THINK they know can help us deepen what they really DO know!
Now…for one other little bit of news! Today I am honored to have a blog post about teaching math perseverance featured on “Minds In Bloom”–one of the BEST blogs around for sharing great teaching ideas! Interested in reading it and checking out the freebie I have included?
Click
HERE to go to Minds in Bloom to see my featured post! Have a great Sunday, everyone!