Hello and Happy Sunday!
Thanks to ALL of you so much for your support of my fraction unit! I was so happy to see so many of you were able to get it yesterday. . . and the kind comments you left just made my day. Thanks so much . . . hopefully lots of students will be having fun learning fractions in a really meaningful way!
I didn’t really blog much about my little mini unit on angles and protractors . . . I do have something kind of fun to share with that, but I do want to start digging into division. Now, if you have taught intermediate level students before, you know that this topic can take even the best math student down! Over the next few weeks I’ll try to share some of the lessons I try as I work to really help my students understand the concept of division and sharing as well as what to do with those pesky remainders!
So, to start, I asked my students to spend a few minutes journaling about what they understand about division. We did a little sharing, and I found out that the kids knew a little–but didn’t really have much to say!
We did have a few students who made the connection to multiplication and most were able to talk briefly about “sharing”. Now, here is where I might be a little different than some teachers. It’s time for me to ask my first division problem. 4 divided by 2? 10 divided by 5? Nope.
“Four children find a five dollar bill. How can they share it? Explain clearly.”
See? Isn’t that WAY more fun? I told the students that I thought with careful thought that they would be able to solve this problem quite quickly–and they did. What I was really after, I explained, what that they work to apply all of those math practice standards that we have been studying this year–so I expected to see precision, organized work, labels, and so on.
And so they worked and worked and drew and drew and labeled and labeled. . . I walked around to ask questions and to “notice” things. When they finished working in their notebooks, I asked them to transfer their ideas even more clearly to a learning poster.
I had my eye on a few that I wanted to share with the class, and I snagged them when they were finished. As they finished, I asked them to try this problem:
“Six children find a five dollar bill. How do they share it?”
Immediately those early finishers started pairing up to tackle this one–I was happy to see that they instantly knew that this was not going to work out quite as nicely!
As I noticed that most of the class was finishing, I called everyone to the front and told them that we were going to play a guessing game. I was going to flash a learning poster on the Smartboard, and they were going to guess WHY I selected it. I explained that I hadn’t even really looked at answers although I was pretty confident that they were correct–I wanted them to think about it through the lens of the math practices.
Here was the first one:
The students all agreed that I probably selected it because the math was clearly organized and the explanation was kept separate. I agreed.
Here are some of the others I selected. See if you can tell why I picked them!
 |
| This student showed several different ways to solve the problem…I thought that was pretty cool! |
 |
| This student took the time to use a straightedge to make straight lines for his explanation. He is NOT known for taking his time so this was a big step. He made me promise he would get it back to show his dad. |
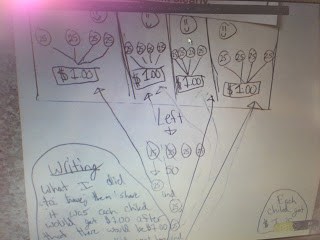 |
| This student used arrows that lined up with her explanation to really make sure we could tell what she was doing. |
 |
| This student started out by solving the problem quite quickly . . . but then had second thoughts and documented “NEW” thinking — see below. |
It was a GREAT first day of division! The students loved talking about each other’s work–and one of the coolest things EVER was that I heard several different students giving compliments to some of the “showcased” students after we finished–not because I told them too–but because they genuinely appreciated their math work. How cool is THAT?
I quickly want to mention the last student’s work. This student solved this problem with ease in his notebook and wanted to work on the challenge problem. I asked him if he was really ready to transfer his work to his learning m frantically working. I let him work for a bit and then went over to investigate. He said to me, “Well, I was thinking. The problem never said that the kids shared the money equally.” Sure enough. It didn’t.
If you can’t read it in the photo, his explanation says, “I knew if there was four kids, one would’ve found it so the finder gets $1.70 and the others get $1.10.”
I don’t know which was more exciting to me–the fact that he thought outside of the box or the fact that he RECOGNIZED that his ideas had changed and he noted that on his learning poster. Math can be so much fun! Thanks again for all your support over the months, everyone. Have a wonderful Sunday!
Missed the link to the Fractions Unit? Here it is one last time. . .















